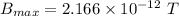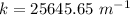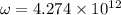Question

An electromagnetic wave in a vacuum traveling in the +x direction generated by a variable source initially has a wavelength λ of 245 μm and a maximum electric field Emax in the +y direction of 6.50×10−3 V/m . If the period of the wave is then increased by a factor of 1.80, what is the equation of the resulting magnetic field component of the wave?

Answer 1

The resulting magnetic field component of the wave

`B_(max)=2.166*10^(-12)\ T`

`k =25645.65\ m^(-1)`

`\omega =4.274*10^(12)`

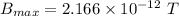
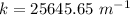
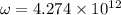
Step-by-step explanation:

Given that,

Wavelength = 245 μm

Electric field
`E= 6.50*10^(-3)\ V/m`

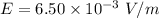
We need to calculate the wave number and angular frequency

Using formula of wave number

`k=(2\pi)/(\lambda)`

`k=(2\pi)/(245*10^(-6))`

`k=25645.65\ m^(-1)`

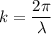
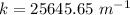
The angular frequency is

`\omega_(0)=(2\pi)/(T)`

`\omega_(0)=(2\pi)/((\lambda)/(c))`

`\omega_(0)=25645.65*3*10^(8)`

`\omega_(0)=7.693695*10^(12)\ rad/sec`

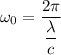
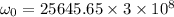
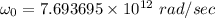
If the wave period increases by a factor of 1.80 times

`\omega=(2\pi)/(1.80T)`

`\omega=(\omega_(0))/(1.80)`

`\omega=(7.693695*10^(12))/(1.80)`

`\omega=4.274*10^(12)\ rad/sec`

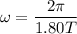
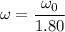
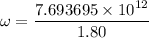
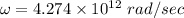
The maximum
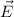`\vec{E}` and
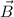`\vec{B}` related by the equation

`B_(max)=(E_(max))/(c)`

Put the value in the equation

`B_(max)=(6.50*10^(-3))/(3*10^(8))`

`B_(max)=2.166*10^(-12)\ T`

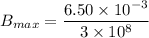
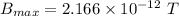
The magnetic field is perpendicular to the electric field.

So, the equation is

`B=[2.166*10^(-12)]exp(25645.65\ x-4.274*10^(12)\ t). \hat{Z}`

Hence, The resulting magnetic field component of the wave

`B_(max)=2.166*10^(-12)\ T`

`k =25645.65\ m^(-1)`

`\omega =4.274*10^(12)`