Question

A rock is suspended from a string, and it accelerates downward. Which one of the following statements is correct? Group of answer choices

a. The magnitude of the tension in the string is greater than the magnitude of the weight of the rock.
b. The magnitude of the tension in the string is independent of the magnitude of the rock's acceleration..
c. The magnitude of the tension in the string is equal to the magnitude of the weight of the rock.
d. The string pushes downward on the rock.
e. The magnitude of the tension in the string is less than the magnitude of the weight of the rock.

Answer 1

a. The magnitude of the tension in the string is greater than the magnitude of the weight of the rock.

Step-by-step explanation:

During the motion of the rock while it is in downward motion we can say

`T - mg cos\theta = ma_c`

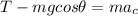
since it is performing circular motion so we will have its acceleration towards its center

`T = mgcos\theta + ma_c`

`a_c = (v^2)/(L)`

`T = mgcos\theta + (mv^2)/(L)`

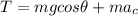
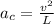
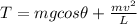
So at the lowest point of the path we can say

`T = mg + (mv^2)/(L)`

so correct answer is

a. The magnitude of the tension in the string is greater than the magnitude of the weight of the rock.