Question

The Arrhenius equation shows the relationship between the rate constant k and the temperature T in kelvins and is typically written as k=Ae−Ea/RT where R is the gas constant (8.314 J/mol⋅K), A is a constant called the frequency factor, and Ea is the activation energy for the reaction. However, a more practical form of this equation is lnk2k1=EaR(1T1−1T2) which is mathematically equivalent to lnk1k2=EaR(1T2−1T1) where k1 and k2 are the rate constants for a single reaction at two different absolute temperatures (T1 and T2). Part A The activation energy of a certain reaction is 45.6 kJ/mol . At 30 ∘C , the rate constant is 0.0160s−1 . At what temperature in degrees Celsius would this reaction go twice as fast

Answer 1

Step-by-step explanation:

2t2 is 1 1t1 = 11 11t2

1212t12 = 0 0t2=2 der fo it 2

Answer 2

T = 42.08 °C

Step-by-step explanation:

Using the expression,

`\ln (k_(1))/(k_(2)) =-(E_(a))/(R) \left ((1)/(T_1)-(1)/(T_2) \right )`

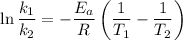
Wherem

`k_1\ is\ the\ rate\ constant\ at\ T_1`

`k_2\ is\ the\ rate\ constant\ at\ T_2`

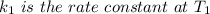
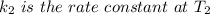
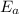`E_a` is the activation energy

R is Gas constant having value = 8.314 J / K mol

Thus, given that,
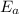`E_a` = 45.6 kJ/mol = 45600 J/mol (As 1 kJ = 1000 J)

`k_2=2* k_1`

`k_1=0.0160s^(-1)`

`T_1=30\ ^0C`

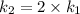
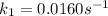
The conversion of T( °C) to T(K) is shown below:

T(K) = T( °C) + 273.15

So,

T = (30 + 273.15) K = 303.15 K

`T_1=303.15\ K`

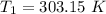
So,

`\ln (k_(1))/(2* k_(1)) =-(45600)/(8.314) \left ((1)/(303.15)-(1)/(T_2) \right )`

`\ln (1)/(2) =-(45600)/(8.314) \left ((1)/(303.15)-(1)/(T_2) \right )`

`8.314\ln \left(2\right)=-45600\left((1)/(303.15)-(1)/(T_2)\right)`

`8.314\ln \left(2\right)=-150.42058+(45600)/(T_2)`

`144.65775 =(45600)/(T_2)`

`T_2=(45600)/(144.65775)`

`T_2=315.23\ K`

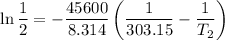
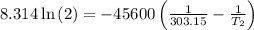
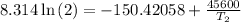
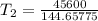
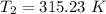
Conversion to °C as:

T(K) = T( °C) + 273.15

So,

315.23 = T( °C) + 273.15

T = 42.08 °C