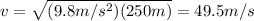Question

In Fig. 6-57, a stuntman drives a car (without negative lift) over the top of a hill, the cross section of which can be approximated by a circleofradiusR????250m.Whatis the greatest speed at which he can drive without the car leaving the road at the top of the hill?

Answer 1

49.5m/s

Step-by-step explanation:

The vertical force must be equal to the centripetal force. In the limit case when the contact force is just 0N (just almost leaving the ground, slower there is more contact and faster will leave the ground) the only vertical force acting on the car will be its weight, so this must be equal to the centripetal force
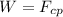`W=F_(cp)`, and then we use the definition of weight and the equation for centripetal force:

`mg=mv^2/r`

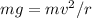
And solve for the velocity:

`v=√(gr)`

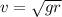
Using our values:

`v=√((9.8m/s^2)(250m))=49.5m/s`