Question

At the top of a cliff 100 m high, Raoul throws a rock upward with velocity 15 m/s. How much later should he drop a second rock from rest so both rocks arrive simultaneously at the bottom of the cliff?

a. 5.05 s
b. 3.76 s
c. 2.67 s
d. 1.78 s

Answer 1

d. 1.78s

Step-by-step explanation:

The total time in the air for the second rock can be found with the next equation:

`h=v_(o)t+(1)/(2) gt^2`

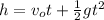
where
`h` is the height, in this case 100m

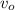`v_(o)` the inicitial velocity wich is 0 since it came from rest

g is gravity and t is time

So we have:

`100=(1)/(2)(9.8m/s^2)t^2`

`t= \sqrt{(200m)/(9.8m/s^2) } =4.52s`

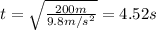
For the fist rock we need to find the time it takes to go up and go back down to the height it was launched:

that time is

`t_(1)=2v_(o)/g =2(15m/s)/9.8m/s^2=3.06s`

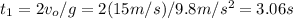
and the time the fist rock is going down from that point, we can find in a similar way we did for the fist rock,
`t_(2)` is:

`h=v_(o)t+(1)/(2) gt^2`

`100=(15m/s)t_(2)+(1)/(2)(9.8m/s^2)t_(2)^2\\0=-100 + (15m/s)t_(2)+(1)/(2)(9.8m/s^2)t_(2)^2`

`0=-100 + (15m/s)t_(2)+(4.9m/s^2)t_(2)^2`

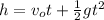
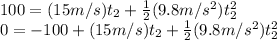
solving as a quadratic equation for time we get:

`t_(2)=3.24s`

So, the total time for the first rock is:

`t_(1)+t_(2)= 3.06s + 3.24s =6.3s`

This means that the second rock must be dropped 6.3s - 4.52 s = 1.78 seconds later, wich is the difference in the times that it takes for each rock to get to the bottom if the cliff.