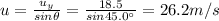Question

A historical society is testing an old cannon. They

place the cannon in an open, level field and perform
a few test fires to determine the speed at which the
cannonballs leave the cannon. The cannon is placed
at a 45.0° angle from the horizontal and placed in a
bunker so that the cannonballs are fired from ground
level. They measure the flight time of one cannonball
to be 3.78 s. (2.3) m
(a) What is the speed of the cannonball as it leaves
the cannon?

Answer 1

26.2 m/s

Step-by-step explanation:

We can find the speed of the cannonball just by analyzing its vertical motion. In fact, the initial vertical velocity is

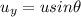`u_y = u sin \theta` (1)

where u is the initial speed and
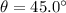`\theta = 45.0^(\circ)` is the angle of projection.

We can therefore use the following suvat equation for the vertical motion of the ball:

`v_y = u_y + at`

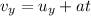
where
`v_y` is the vertical velocity at time t, and
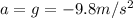`a=g=-9.8 m/s^2` is the acceleration of gravity. The time of flight is 3.78 s, so we know that the ball reaches its maximum height at half this time:

`t=(3.78)/(2)=1.89 s`

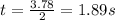
And at the maximum height, the vertical velocity is zero:

`v_y=0`

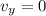
Substituting these values, we find the initial vertical velocity:

`u_y = v_y - at = 0-(-9.8)(1.89)=18.5 m/s`

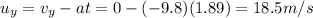
And using eq.(1) we now find the initial speed:

`u=(u_y)/(sin \theta)=(18.5)/(sin 45.0^(\circ))=26.2 m/s`