Question

A particle of mass m is placed in a three-dimensional rectangular box with edge lengths 2L, L, and L. Inside the box the potential energy is zero, and outside it is infinite; therefore, the wave function goes smoothly to zero at the sides of the box. Calculate the energies and give the quantum numbers of the ground state and the first five excited states (or sets of states of equal energy) for the particle in the box.

Answer 1

E = (h2 / 8mL2) (n1² /4 + n2² + n3²) ground state (1 0 0)

Step-by-step explanation:

The solution of the Schrödinger equation for a potential box with infinite walls is a relatively simple state described in one dimension by the equation

E = (h² / 8mL²) n²

Where h is the Planck constant 6.63 10 -34 J s, m the mass of the particle, L the length of the box, n is an integer that in quantum mechanics is called quantum number

Let's apply this equation to our case

X axis

E = (h² / 8mLₓ²) n1²

Lx = 2L

E1 = (h² / 8m (2L)²) n1²

E1 = (h² / 8mL²) ¼ n1²

Y Axis

E2 = (h² / 8m
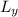`L_(y)`²) n2²

Ly = L

E2 = (h2 / 8mL²) n2²

Z axis

E3 = (h2 / 8m
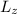`L_(z)`²) n3²

Lz = L

E3 = (h² / 8mL²) n3²

As energy is a scalar and is additive

E = E1 + E2 + E3

E = (h² / 8mL²)) ¼ n1² + (h² / 8mL²) n2² + (h² / 8mL²)) n3²

Let's simplify

E = (h2 / 8mL2) (n1² /4 + n2² + n3²)

Let's call Eo = (h² / 8mL²) to simplify the equation a bit

E = Eo (1/4 n1²+ n2² + n3²)

The base state is the lowest energy state

If we inspect the equation above the state of lowest energy acure for

n1 = 1 n2 = 0 n3 = 0

E = (h² / 8mL²) (¼ + 0 +0)

E = ¼ Eo

The first excited states are

n1 n2 n3 E

0 0 1 Eo

0 1 0 Eo

1 0 1 E0 (1+ ¼) = 5/4 Eo

1 1 0 5/4 Eo

1 1 1 Eo (¼ + 1 + 1) = 9/4 Eo