Question

Suppose babies born after a gestation period of 32 to 35 weeks have a mean weight of 2500 grams and a standard deviation of 700 grams while babies born after a gestation period of 40 weeks have a mean weight of 3000 grams and a standard deviation of 475 grams. If a 34​-week gestation period baby weighs 2975 grams and a 41​-week gestation period baby weighs 3475 ​grams, find the corresponding​ z-scores. Which baby weighs more relative to the gestation​ period?

Answer 1

The 41 week gestation's period baby has a higher zscore, so he weighs more relative to the gestation​ period.

Explanation:

Normal model problems can be solved by the zscore formula.

On a normaly distributed set with mean
`\mu` and standard deviation
`sigma`, the z-score of a value X is given by:

`Z = (X - \mu)/(\sigma)`

The zscore represents how many standard deviations the value of X is above or below the mean
`\mu`.

In this problem, whichever baby has the higher zscore is the one who weighs more relative to the gestation period.

Babies born after a gestation period of 32 to 35 weeks have a mean weight of 2500 grams and a standard deviation of 700 grams. A 34-week gestation period baby weighs 2975.

Here, we have
`\mu = 2500, \sigma = 700, X = 2975`.

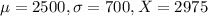So

`Z = (X - \mu)/(\sigma)`

`Z = (2975 - 2500)/(700)`

`Z = 0.68`

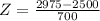
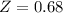
Babies born after a gestation period of 32 to 35 weeks have a mean weight of 3000 grams and a standard deviation of 475 grams. A 41-week gestation period baby weighs 3475.

Here, we have
`\mu = 3000, \sigma = 475, X = 3475`.

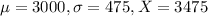So

`Z = (X - \mu)/(\sigma)`

`Z = (3475 - 3000)/(475)`

`Z = 1`

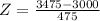
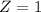
The 41 week gestation's period baby has a higher zscore, so he weighs more relative to the gestation​ period.