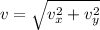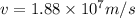Question

An electron (e = 1.6 x 10-19 C, me = 9.11 x 10-31 kg) begins at rest with potential energy 1.6 x 10-16 J and is accelerated to its final speed (with no potential energy) before entering a region of constant electric field of 5000 N/C between two parallel plates. The plates are separated by a distance d = 2 cm, and each has a length l = 4 cm. The electron enters the region moving parallel to the plates, exactly half-way between the two. Does the electron collide with either of the plates? If yes, where (at what horizontal distance) does it strike a plate, and how fast is it moving before it does so? If no, by what (vertical) distance is it deflected and how fast is it moving as it leaves the region between the plates

Answer 1

electron will not strike any plate and its displacement in vertical direction is 0.201 mm

`v = 1.88 * 10^7 m/s`

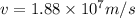
Step-by-step explanation:

As we know that whole potential energy of electron will convert into kinetic energy

So here we will have

`1.6 * 10^(-16) = (1)/(2)mv^2`

`v = 1.87 * 10^7 m/s`

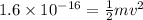
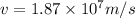
Now we know that time to cross the plates is given as

`x = v_x t`

`0.04 = (1.87 * 10^7) t`

`t = 2.14 * 10^(-9) s`

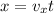
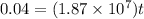
now in vertical direction acceleration of electron is given as

`a = (qE)/(m)`

`a = ((1.6 * 10^(-19) 5000)/(9.11 * 10^(-31))`

`a = 8.8 * 10^(14) m/s^2`

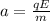
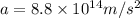
now its vertical displacement is given in same time

`y = (1)/(2)at^2`

`y = 2.01 * 10^[-3} m`

`y = 0.201 mm`

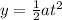
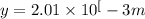
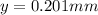
So electron will not strike any plate and its displacement in vertical direction is 0.201 mm

As it leaves the plate the velocity in x direction will remain constant

`v_x = 1.87 * 10^7 m/s`

`v_y = at`

`v_y = (8.8 * 10^(14))(2.14 * 10^(-9))`

`v_y = 1.88 * 10^6 m/s`

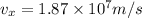
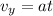
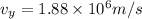
Now net speed is given as

`v = √(v_x^2 + v_y^2)`

`v = 1.88 * 10^7 m/s`