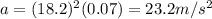Answer:
Step-by-step explanation:
First of all, we need to convert the angular velocity from revolutions per second to radiands per second. We know that
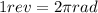
So
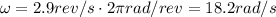
We also know that the distance of the inner ear from the centre of the circular path is
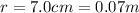
the radial (centripetal) acceleration experienced by a point on the inner ear is
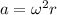
Therefore, substutiting the previous values, we find the radial acceleration of the endolymph fluid: