Answer: The correct option is
(A)
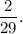
Step-by-step explanation: Given that in a bag of 30 cookies, there are 12 chocolate chip, 4 double chocolate chip, 5 peanut butter, 3 sugar, and 6 mint chocolate cookies.
Sarah reaches in and takes a 2 cookies and eats them.
We are to find the probability that she picked a chocolate chip cookie and then a peanut butter cookie. Also, to check whether these events are independent or dependent.
Let A denotes the event that Sarah picks a chocolate chip cookie and B denotes the event that Sarah picks a peanut butter cookie.
So, the probabilities of events A and B are
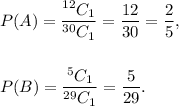
Since the number of total cookies is reduced by one after Sarah picked and ate chocolate chip cookie, so
event B is dependent on event A.
Therefore, the events are dependent and the probability that Sarah picked a chocolate chip cookie and then a peanut butter cookie is

Thus, the required probability is
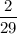 and the events are dependent.
and the events are dependent.
Option (A) is CORRECT.