Question

If a baseball player hits a baseball from 4 feet off the ground with an initial velocity of 64 feet per second, how long will it take the baseball to hit the ground? Use the equation h = −16t2 + 4t + 4. Round your answer to the nearest hundredth. 0.36 0.39 0.61 0.64

Answer 1

0.64

Explanation:

I got right on the test.

Answer 2

0.64s

Explanation:

Hello!

To solve this problem we must use the equation to determine for what time (t), the ball touches the ground that is when h = 0

`h =-16t^2 + 4t + 4\\for h=0\\0=-16t^2 + 4t + 4\\`

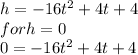
Now we have a quadratic equation, which has two answers, for this we use the following equation

a = number that accompanies the variable t ^ 2

=-16

b = number that accompanies the variable t

=4

c = independent number of t=4

`t=(-b+√(b^2-4ac) )/(2a)`

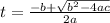
solving

`t=\frac{-4(-+)\sqrt[2]{4^2-4(-16)(4)} }{2(-16)}`

remember that when the equation is quadratic it has two answers, one with the sign (+), and another with the sign (-), you choose the positive result since it is impossible for the time to be negative

t1=0.64s

t2=-0.39s

answer=0.64s