2 Answers

Sevensevens · Answer 1 · 2020-02-13T18:30:51+0000

Option B is correct.

ANSWER:

The equation in slope-intercept form, of the line that passes through (0, 6) and has a slope of 4 is y = 4x + 6

SOLUTION:

Given, Point P (0, 6) and slope = 4

We need to find the equation in Slope-intercept form.

The slope intercept form is given as y = mx + c -------- eqn (1)

Where, m is the slope of line

C is intercept made on x-axis by the line.

We have a point and the slope, so first we can find equation using point-slope form and then convert into slope-intercept form.

Now, point-slope form is given as
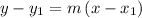$y-y_(1)=m\left(x-x_(1)\right)$ --- eqn 2

Put
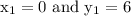$\mathrm{x}_(1)=0 \text { and } \mathrm{y}_(1)=6$ in eqn (2) along with m = 4

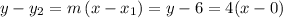
$y-y_(2)=m\left(x-x_(1)\right)=y-6=4(x-0)$

y – 6 = 4x

We got the equation in point slope form, now let’s convert it into slope intercept form.

y – 6 = 4x

y = 4x + 6

Here, slope (m) = 4 and intercept (c) = 6

Hence we can conclude that, equation, in slope-intercept form, of the line that passes through (0, 6) and has a slope of 4 is y = 4x + 6

Please log in or register to add a comment.