Answer:
The correct answer is option C,
Explanation:
Hose-A fills 60 gallons of water in 15 minutes .
Rate of Hose-A at which it fills water truck =

Hose-B fills water truck , its function is given as:
y = 3x
Where y is the total number of gallons filled in x minutes.
Rate of Hose-B at which it fills water truck =
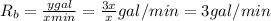
Difference in rates of both hoses:

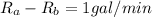
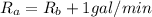
The rate of Hose A is 1 gallon per minute more than the rate of Hose B.