Question

A faucet is used to add water to a large bottle that already contained some water. After it has been filling for 55 ​seconds, the gauge on the bottle indicates that it contains 1919 ounces of water. After it has been filling for 1111 ​seconds, the gauge indicates the bottle contains 3737 ounces of water. Let y be the amount of water in the bottle x seconds after the faucet was turned on. Write a linear equation that relates the amount of water in the​ bottle, y, to the time x.

Answer 1

`y=3x+4`

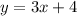
Explanation:

Let y be the amount of water in the bottle x seconds after the faucet was turned on.

We have been given that the gauge on the bottle indicates that it contains 19 ounces of water after it has been filling for 5 seconds. After it has been filling for 11 ​seconds, the gauge indicates the bottle contains 37 ounces of water.

We have two points on the line
`(5,19)` and
`(11,37)`.

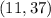Let us find slope of the line passing through these points.

`m=(y_2-y_1)/(x_2-x_1)`

`m=(37-19)/(11-5)`

`m=(18)/(6)`

`m=3`

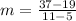
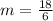
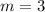
We will write our required equation in slope-intercept form
`y=mx+b`, where, m represents slope and b represents the y-intercept.

Let us find y-intercept by substituting
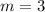`m=3` and coordinates of point
`(5,19)` in slope intercept form.

`19=3\cdot 5+b`

`19=15+b`

`19-15=15-15+b`

`4=b`

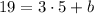
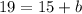
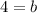
Therefore, our required equation would be
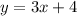`y=3x+4`.