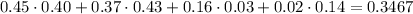Answer:
A. 0.14
B. 0.0048
C. 0.3467
Explanation:
You are given the table

The sum in each row must be equal to 1, so
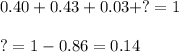
Hence, the table is

A. The probability that a person from Midwest has Discover card is
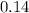
B. The probability that a person chosen at random from East Coast and Midwest, independently of one another, both have type American Express is
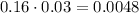
C. The probability that a person chosen at random from East Coast and Midwest, independently of one another, both have the same type of credit card is