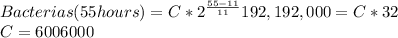Question

A colony of bacteria is grown under ideal conditions in a laboratory so that the population increases exponentially with time. At the end of 55 hours there are 192192​,000 bacteria. At the end of 66 hours there are 384384​,000. How many bacteria were present​ initially?

Answer 1

Initial bacterias = 6006000

Altought I believe is safe to assume that the values were 192,000 and 384,000 instead of 192,192,000 and 384,384,000, in that case the initial bacterias is 6000

Explanation:

A exponential growth follows this formula:

Bacterias = C*rⁿ

C the initial amount

r the growth rate

n the number of time intervals

Bacterias (55 hours) = 192,192,000

Bacterias (66 hours) = 384,384,000

`Bacterias(55hours)=C*r^{{(55-t)/(t)}} \\Bacterias (66hours) = C*r^{(66-t)/(t)}}`

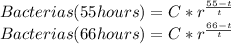
If you divide both you can get the growth rate:

`(Bacterias (66hours))/(Bacterias(55hours))=\frac{C*r^{(66-t)/(t)}}{C*r^{{(55-t)/(t)}}} \\(384,384,000)/(192,192,000) =r^{(66-t)/(t) -(55-t)/(t) } \\2 =r^{(11)/(t)}`

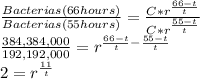
So with that r = 2 and each time interval correspond to 11 years

Then replacing in one you can get the initial amount of C

`Bacterias (55hours)=C*2^{(55-11)/(11) } 192,192,000 = C*32\\C= 6006000`