Question

The mean life of a particular brand of light bulb is 1200 hours. If you know that at about 95% of this brand of bulbs will last between 1100 and 1300 hours, then what is the standard deviation of the light bulbs’ life?​

​a) 200
​b) 100
​c) 50
​d) 25
​e) 75

Answer 1

c) 50

Explanation:

We have been given that the mean life of a particular brand of light bulb is 1200 hours. About 95% of this brand of bulbs will last between 1100 and 1300 hours.

We will use z-score formula to solve our given problem.

`z=(x-\mu)/(\sigma)`, where,

`z=\text{z-score}`,

`x=\text{Sample score}`,

`\mu=\text{Mean}`,

`\sigma=\text{Standard deviation}`

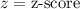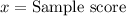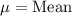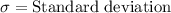
We know that 95% of data points lies within two standard deviation of mean, so 1100 will correspond to a z-score of -2 and 1300 will correspond to a z-score of 2.

`-2=(1000-1200)/(\sigma)`

`-2=(-100)/(\sigma)`

`\sigma=(-100)/(-2)`

`\sigma=50`

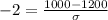
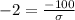
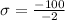
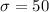
We can use sample score 1300 and get same answer as:

`2=(1300-1200)/(\sigma)`

`2=(100)/(\sigma)`

`\sigma=(100)/(2)`

`\sigma=50`

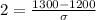
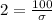
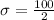
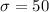
Therefore, the standard deviation of the light bulbs’ life is 50 years.