Question

Two cars travel in the same direction along a straight highway, one at a constant speed of 57 mi/h and the other at 76 mi/h. Assuming they start at the same point, how much sooner does the faster car arrive at a destination 12 mi away? Answer in units of min. How far must the faster car travel before it has a 20 min lead on the slower car? Answer in units of mi.

Answer 1

Car 2 arrives 3.16 minutes sooner to car 1 at 12 miles.

The faster car must travel 75.76 miles before it has a 20 min lead on the slower car.

Explanation:

Speed of car 1 = 57 mph

Speed of car 2 = 76 mph

We need to find how much sooner does the faster car arrive at a destination 12 mi away.

Time taken for car 1

`t_1=(12)/(57)=0.21hour=12.63minutes`

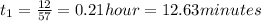
Time taken for car 2

`t_2=(12)/(76)=0.158hour=9.47minutes`

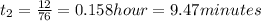
Difference between arrival = 12.63 - 9.47 = 3.16 minutes

So the car 2 arrives 3.16 minutes sooner to car 1 at 12 miles.

Now we need to find the distance at which faster car has a 20 minute lead

Difference between arrival = 20 minutes

Let the distance be S

Time taken for car 1

`t_1=(S* 60)/(57)=1.053S`

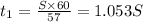
Time taken for car 2

`t_2=(S* 60)/(76)=0.789S`

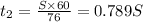
We have

1.053 S - 0.789 S = 20

S = 75.76 miles

So the faster car must travel 75.76 miles before it has a 20 min lead on the slower car.