Question

Consider a multiple choice exam with 10 questions, and with 4 possible answers to each question (labeled A, B, C, and D). 1a. What is the probability of getting a perfect score just by guessing? 1b. What is the probability of getting at least one question correct, just by guessing? Explain your thought process briefly. 2. Each RUID is 9-digits long, but the 4th and 5th digits must both be 0. How many different RUIDs can there be?

Answer 1

(1a) 9.54e-07 (1b) 0.9437 (2)
`10^8`

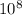
Explanation:

We have n = 10 questions. For each question in the multiple choice exam, we can choose the correct answer with probability p = 0.25 or an incorrect answer with probability q = 0.75 (just by guessing). Besides is reasonable to believe that questions are independent. Let X be the random variable that represents the number of correct answers (just by guessing) observed during the n = 10 questions, so, X have a binomial distribution.

(a) The probability of getting a perfect score just by guessing is

`P(X = 10) = 10C10(0.25)^(10)(0.75)^(10-10) = 9.54e-07`

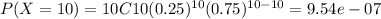
(b) The probability of getting at least one question correct, just by guessing

`P(X\geq1) = \sum_(x=1)^(x=10)10Cx(0.25)^(x)(0.75)^((10-x)) = 0.9437`

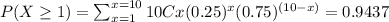
2. Each RUID is 9-digits long, there are 10 digits, each of the nine positions for a digit of the RUID has 10 posibilities except the 4th and 5th positions which must be both 0. For the multiplication rule there can be
`(10)^3(1)(1)(10)^5 = 10^8` different RUIDS.