Question

A ball of moist clay falls 17.0 m to the ground. It is in contact with the ground for 19.0 ms before stopping,

(a) What is the average acceleration of the ball during the time it is in contact with the ground? (Treat the ball as a particle.)
(b) Is the average acceleration up or down?

Answer 1

Step-by-step explanation:

It is given that,

Initial height of the ball,
`x_o=17\ m`

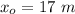
As it stops, its position, x = 0

It is in contact with the ground for 19.0 ms before stopping,
`t=19* 10^(-3)\ s`

Initial speed of the ball, u = 0

(a) Let a is the acceleration of the ball during the time it is in contact with the ground. Its can be calculated suing equation of kinematics as :

`v^2-u^2=2a(x-x_o)`

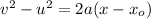
a =-g

`v^2=-2g(x-x_o)`

`v^2=-2g(-17)`

`v^2=-2* 9.8* (-17)`

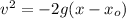
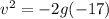
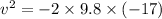
v = 18.25 m/s

(b) The average acceleration can be calculated as :

`a_(avg)=(v-u)/(t)`

`a_(avg)=(18.25-0)/(19* 10^(-3))`

`a_(avg)=960.52\ m/s^2`

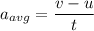
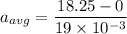
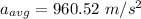
As the value of acceleration is positive, so the ball is accelerating in upward direction.