Question

The number of home runs scored by a certain team in one baseball game is a random variable with the distribution x 0 1 2 P(x) 0.4 0.4 0.2 The team plays 2 games. The number of home runs scored in one game is independent of the number of home runs in the other game. Let Y be the total number of home runs. Find E(Y ) and Var(Y ).

Answer 1

Answer: E(Y) = 1.6 and Var(Y)=1.12

Explanation:

Since we have given that

X 0 1 2

P(X) 0.4 0.4 0.2

Here, number of games = 2

So,
`Y=X_1+X_2`

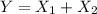
Since
`X_1\ and\ X_2` are independent variables.

so,
`E[Y]=2E[X]\\\\Var[Y]=2Var[X]`

So, we get that

`E(X)=0.4* 0+0.4* 1+0.2* 2=0.8\\\\and Var[x]=E[x^2]-(E[x])^2\\\\E[x^2]=0* 0.4+1* 0.4+4* 0.2=1.2\\\\So, Var[x]=1.2-(0.8)^2\\\\Var[x]=1.2-0.64=0.56`

So, E[y]=2×0.8=1.6

and Var[y]=2×0.56=1.12

Hence, E(Y) = 1.6 and Var(Y)=1.12