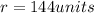Question

Find the length of the following​ two-dimensional curve. r (t ) = (1/2 t^2, 1/3(2t+1)^3/2) for 0 < t < 16

Answer 1

To find the arc length of the curve r(t) = (1/2 t^2, 1/3(2t+1)^3/2) for 0 < t < 16, calculate the speed by finding the derivative of r(t), then integrate the speed from t=0 to t=16.

Step-by-step explanation:

To find the length of the two-dimensional curve r(t) = (\frac{1}{2} t^2, \frac{1}{3}(2t+1)^{\frac{3}{2}}) for 0 < t < 16, we need to calculate the integral of the curve's speed from t=0 to t=16.

1. First, compute the derivative of r(t) with respect to time to obtain the velocity vector, v(t).
2. The velocity vector v(t) is given by the derivative of each component of r(t): v(t) = (\frac{1}{2}*2t, \frac{1}{3}*\frac{3}{2}*(2t+1)^{\frac{1}{2}}*2), which simplifies to v(t) = (t, (2t + 1)/\sqrt{2t + 1}).
3. Next, calculate the speed, which is the magnitude of the velocity vector, by taking the square root of the sum of the squares of the components of v(t).
4. Speed(t) = \sqrt{t^2 + (\frac{2t + 1}{\sqrt{2t + 1}})^2} = \sqrt{t^2+(2t+1)^2/(2t+1)} = \sqrt{t^2+2t+1}.
5. Finally, integrate the speed from t=0 to t=16 to find the arc length, using the formula \int_0^{16} \sqrt{t^2+2t+1} dt.

Completing this integral will give the total arc length of the curve over the given interval for t.

Answer 2

r = 144 units

Step-by-step explanation:

The given curve corresponds to a parametric function in which the Cartesian coordinates are written in terms of a parameter "t". In that sense, any change in x can also change in y owing to this direct relationship with "t". To find the length of the curve is useful the following expression;

`r(t)=\int\limits^a_b ({r`)^2 \, dt =\int\limits^b_a \sqrt{(((dx)/(dt) )^2 +(dy)/(dt) )^2)} dt`

In agreement with the given data from the exercise, the length of the curve is found in between two points, namely 0 < t < 16. In that case a=0 and b=16. The concept of the integral involves the sum of different areas at between the interval points, although this technique is powerful, it would be more convenient to use the integral notation written above.

Substituting the terms of the equation and the derivative of r´, as follows,

`r(t)= \int\limits^b_a \sqrt{(((d((1/2)t^2))/(dt) )^2 +(d((1/3)(2t+1)^(3/2)))/(dt) )^2)} dt`

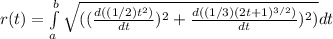
Doing the operations inside of the brackets the derivatives are:

1 )
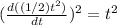
`((d((1/2)t^2))/(dt) )^2= t^2`

2)
`((d(1/3)(2t+1)^(3/2)))/(dt) )^2=2t+1`

Entering these values of the integral is

`r(t)= \int\limits^(16)_(0) √(t^2 +2t+1) dt`

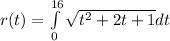
It is possible to factorize the quadratic function and the integral can reduced as,

`r(t)= \int\limits^(16)_(0) (t+1) dt= (t^2)/(2) + t`

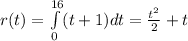
Thus, evaluate from 0 to 16

`(16^2)/(2) + 16`

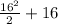
The value is
`r= 144 units`