Answer: 0.48
Explanation:
Given : The probability that a customer will order a hamburger P(H)= 0.60.
The probability that a customer will order french fries P(F)= 0.50.
The restaurant has also determined that if a customer orders a hamburger, the probability the customer will also order fries : P(F|H)= 0.80.
Using conditional probability formula , for any event A (first event) and B (second event), we have:-

Similarly, the probability that the order will include a hamburger and fries :-
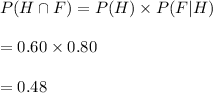
Hence, the probability that the order will include a hamburger and fries=0.48