Option A
ANSWER:
The probability that the surgery is successful for exactly 6 patients is 0.088
SOLUTION:
A surgical technique is performed on 10 patients. You are told there is an 80% chance of success. We have to find the probability that the surgery is successful for exactly 6 patients.
For binomial distribution, the probability mass function for random variable X is given as,

Given, that the total number of patients is n=10
The chance of success for surgical technique is p=80%.
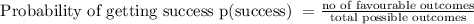
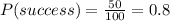
x = 6
The probability for surgery is successful for exactly 6 patients is given by
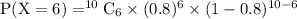
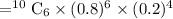
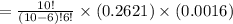
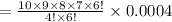
Solving the factorial we get,
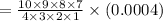
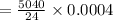
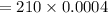
P(X=6) = 0.084
Answer is near to option A. Hence probability that the surgery is successful for exactly 6 patients 0.088.