Question

A surgical technique is performed on 10 patients. You are told there is an 80% chance of success. Find the probability that the surgery is successful for exactly 6 patients.

Group of answer choices

0.088

0.0328

0.1208

0.9672

Answer 1

*100% Correct answers

Question 1

A surgical technique is performed on 10 patients. You are told there is an 80% chance of success. Find the probability that the surgery is successful for exactly 6 patients.

0.088

Question 2

Sam creates a game in which the player rolls 4 dice. What is the probability in this game of having at least 2 of the dice land on 5.

0.13101963141

Question 3

Katie creates a game in which 3 dimes are flipped at the same time.

5 points are awarded if all 3 dimes land on tails, but no points are awarded for anything else. What is the probability of not getting any points? (Hint: Find the complement).

0.875

Answer 2

Probability that the surgery is successful for exactly 6 patients is 0.088.

Explanation:

The total number of patients is 10 and the probability of success is 0.8.

We have to determine the probability of success of the surgery of exactly 6 patients.

6 patients can be selected from 10 patients in
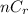`nC_r` ways.

`nC_r=10C_6= \frac {10!}{6!(10-6)!}`

`= (10!)/((6! * 4!))`

`= \frac {3628800}{(720 * 24)}`

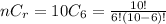
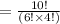
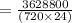
=210

Let us consider a combination SSSSSSFFFF where S denotes success and F denotes failure. The probability of this combination is given by

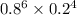`0.8^6 * 0.2^4` since the chance of success is 0.8 and chance of failure is 0.2.

There are 210 such different combinations possible and the probability of every combination is the same. So we have to sum up all the probabilities to determine the final probability.

Therefore the probability that surgery is successful for 6 patients is
`0.8^6 * 0.2^4 * 210=0.088`