Question

Consider the following initial value problem 5 points (1 + t) y’ = t y (4 – y), y(0) = y0 > 0. a) Solve the initial value problem and find its general solution. b) Determine how the solution behaves as t ض. c) If the initial value y0 = 2, find the time T when the solution first reaches the value 3.99.

Answer 1

a) To determine its general solution we have to accommodate the differential equation:

`(dy)/((4-y)y)  = (t*dt)/(t+1)`

We proceed to integrate each part as follow

`(1)/(4) \int\limits {(1)/(y)+(1)/(4-y)} \, dy = \int\limits {1-(1)/(t+1) } \, dt`

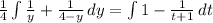
Then we have:

`(Ln((y)/(y-4) ))/(4) = t-Ln(t+1)+C\\\\Ln((y*(t+1)^(4))/(y-4) ) = 4t+4C\\\\(y*(t+1)^(4))/(y-4) = e^(4t+4C) = K*e^(4t)`

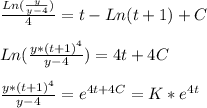
Finally we have:

`y = (4Ke^(4t) )/(Ke^(4t)-(t+1)^(4))`

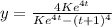
Replacing the initial value y(0) = y0, we have:

K = y0/(y0-4)

b) Please, could you describe better what do you need because I don't understand this "t ض "

c) So we first need to find K, we replace y0=2 and we have:

K = -1

then the equation, replacing y=3.99 is:

`3.99 = (4e^(4t) )/(e^(4t)+(t+1)^(4))`

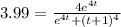
Finally, resolving the equation we have as a result:

t = 2.84