Question

Which of the solution sets is all real numbers?
IXI <-1
IxI= -1
lx|>-1

Answer 1

`|x|>-1`

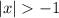
Explanation:

Recall that the function absolute value of any real number gives always a non-negative answer. That is |x| is always
`\geq 0`.

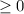Therefore,

1) the first statement will be the empty/Null set (there are no real numbers whose absolute value can be smaller that negative one.

2) Something similar happens with the second statement: the absolute value of a real number cannot be equal to a negative number (in this case "-1". So this set is the empty/Null set.

3) Since we know from our statement above that
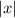`|x|` is always
`\geq 0`,

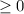and on the other hand 0 is larger than -1 (
`0>-1`)

Then using transitive property, we get:

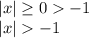`|x|\geq 0>-1\\|x|>-1` which is still true for all real numbers.