Question

Initially, a particle is moving at 5.25 m/s at an angle of 35.5° above the horizontal. Three seconds later, its velocity is 6.03 m/s at an angle of 56.7° below the horizontal. What was the particle's average acceleration during these 3.00 seconds in the x-direction (enter first) and the y-direction?

Answer 1

a =( -0.32 i ^ - 2,697 j ^) m/s²

Step-by-step explanation:

This problem is an exercise of movement in two dimensions, the best way to solve it is to decompose the terms and work each axis independently.

Break down the speeds in two moments

initial

v₀ₓ = v₀ cos θ

v₀ₓ = 5.25 cos 35.5

v₀ₓ = 4.27 m / s

`v_(oy)` = v₀ sin θ

`v_(oy)`= 5.25 sin35.5

`v_(oy)` = 3.05 m / s

Final

vₓ = 6.03 cos (-56.7)

vₓ = 3.31 m / s

`v_(y)` = v₀ sin θ

`v_(y)` = 6.03 sin (-56.7)

`v_(y)` = -5.04 m / s

Having the speeds and the time, we can use the definition of average acceleration that is the change of speed in the time order

a = (
`v_(f)` - v₀) /t

aₓ = (3.31 -4.27)/3

aₓ = -0.32 m/s²

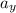`a_(y)` = (-5.04-3.05)/3

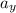`a_(y)` = -2.697 m/s²