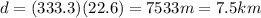a) Time of flight: 22.6 s
To calculate the time it takes for the cargo to reach the ground, we just consider the vertical motion of the cargo.
The vertical position at time t is given by
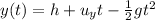
where
h = 2.5 km = 2500 m is the initial height
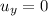 is the initial vertical velocity of the cargo
is the initial vertical velocity of the cargo
g = 9.8 m/s^2 is the acceleration of gravity
The cargo reaches the ground when
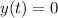
So substituting it into the equation and solving for t, we find the time of flight of the cargo:
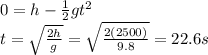
b) 7.5 km
The range travelled by the cargo can be calculated by considering its horizontal motion only. In fact, the horizontal motion is a uniform motion, with constant velocity equal to the initial velocity of the jet:

So the horizontal distance travelled is
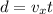
And if we substitute the time of flight,
t = 22.6 s
We find the range of the cargo: