Question

A body moving with uniform acceleration has a velocity of 13 cm/s when its x coordinate is 3.7 cm. If its x coordinate 2.27 s later is −6.3 cm, what is the x-component of its acceleration? Answer in units of cm/s 2 .

Answer 1

Acceleration,
`a=15.33\ m/s^2`

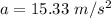
Step-by-step explanation:

Initial speed of the body,
`u=13\ cm/s`

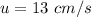
Initial position,
`x_i=3.7\ cm`

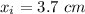
Final position,
`x_f=-6.3\ cm`

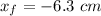
Time taken, t = 2.27 s

We need to find the x-component of its acceleration. Using second equation of kinematics as :

`x_f-x_i=ut+(1)/(2)at^2`

`-6.3-3.7=(13)(2.27)+(1)/(2)(2.27)^2a`

`-10-29.51=(1)/(2)(2.27)^2a`

`a=(-39.51* 2)/((2.27)^2)=-15.33\ m/s^2`

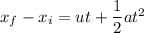
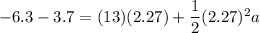
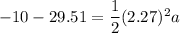
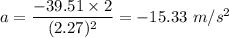
So, the x-component of its acceleration is
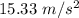`15.33\ m/s^2`. The body is decelerating. Hence, this is the required solution.