Question

Grandma​ Gertrude's Chocolates, a family owned​ business, has an opportunity to supply its product for distribution through a large coffee house chain.​ However, the coffee house chain has certain specifications regarding cacao content as it wishes to advertise the health benefits​ (antioxidants) of the chocolate products it sells. In order to determine the mean percentage of cacao in its dark chocolate​ products, quality inspectors sample 36 pieces. They find a sample mean of​ 60% with a standard deviation of​ 8%. What is the correct value of t to construct a​ 90% confidence interval for the true mean percentage of​ cacao? (Round to the nearest thousandth.)

Select Answer:
A. (0.577, 0.623)
B. (0.539, 0.561)
C. (0.527, 0.573)
D. (0.589, 0.611)

Answer 1

Answer with explanation:

Given : Sample size : n = 36

Significance level for 90% confidence :
`\alpha: 1-0.9=0.1`

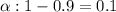
Sample mean :
`\overline{x}=0.60`

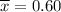
Standard deviation :
`\sigma=0.08`

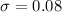
By using standard normal table for t-values,

Critical t-value :
`t_((n-1, \alpha/2))=t_((35,\ 0.05))=1.690`

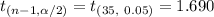
Thus, the correct value of t to construct a​ 90% confidence interval for the true mean percentage of​ cacao :
`t_((35,\ 0.05))=1.690`

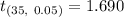
Confidence interval for population mean :

`\overline{x}\pm t_((n-1, \alpha/2))(\sigma)/(√(n))\\\\=0.60\pm(1.69)(0.08)/(√(36))\\\\=0.60\pm0.0225333333333\\\\\approx0.60\pm0.023\\\\=(0.60-0.023,\ 0.60+0.023)=(0.577,\ 0.623)`

Hence, A is the correct answer .