Question

The population of a certain species of bird in a region after t years can be modeled by the function P(t)= 1620/1+1.15e^-0.042t , where t ≥ 0. What is the maximum population of the species in the region?

A. 1,620
B. 1,200
C. 0
D. 720

Answer 1

A.1620

Explanation:

We are given that

`P(t)=(1620)/(1+1.15e^(-0.042t))`

`t\geq 0`

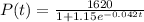
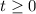
We have to find the maximum population of the species in the region.

We know that

In fraction

Larger the denominator smaller the value of fraction.number.

Substitute t=0

`P(0)=(1620)/(1+1.15e^0)=(1620)/(1+1.15)=753.5`

`P(t)=\lim_(t\rightarrow \infty)(1620)/(1+1.15e^(-0.042t))=(1620)/(1+0)=1620`

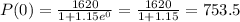
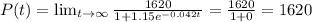
When t increases then the values of
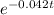`e^(-0.042t)` decreases

As the denominator decreases the value of given function increases.

The maximum population of the species in the region=1620

A.1620

Answer 2

A

Explanation:

The function is
`(1620)/(1+1.15e^(-0.042t))`

To find the maximum population, we need to set t towards infinity to get our answer.

So, we replace time with maximum (
`\infty`). Let's check:

`(1620)/(1+1.15e^(-0.042t))\\=(1620)/(1+(1.15)/(e^(0.042t)))\\=(1620)/(1+(1.15)/(e^(0.042(\infty))))\\=(1620)/(1+(1.15)/(\infty))\\=(1620)/(1+0)\\=(1620)/(1)\\=1620`

The population of birds approaches 1620 as t goes towards infinity. So we can say the max population of the species is 1620.

Correct answer is A