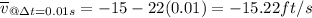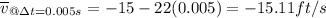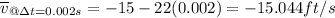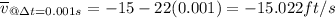Question

A ball is thrown into the air by a baby alien on a planet in the system of Alpha Centauri with a velocity of 29 ft/s. Its height in feet after t seconds is given by y = 29 t − 22 t 2 . A. Find the average velocity for the time period beginning when t=1 and lasting .01 s: .005 s: .002 s: .001 s: NOTE: For the above answers, you may have to enter 6 or 7 significant digits if you are using a calculator.

Answer 1

`\overline{v}_(@\Delta t=0.01s)=-15.22ft/s, \overline{v}_(@\Delta t=0.005s)=-15.11ft/s, \overline{v}_(@\Delta t=0.002s)=-15.044ft/s, \overline{v}_(@\Delta t=0.001s)=-15.022ft/s`

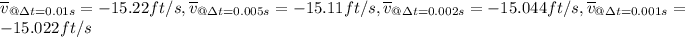
Explanation:

Now, in order to solve this problem, we need to use the average velocity formula:

`\overline{v}=(y_(f)-y_(0))/(t_(f)-t_(0))`

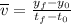
From this point on, you have two possibilities, either you find each individual
`y_(f), y_(0), t_(f), t_(0)` and input them into the formula, or you find a formula you can use to directly input the change of times. I'll take the second approach.

We know that:

`t_(f)-t_(0)=\Delta t`

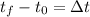
and we also know that:

`t_(f)=t_(0)+\Delta t`

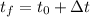
in order to find the final position, we can substitute this final time into the function, so we get:

`y_(f)=29(t_(0)+\Delta t)-22(t_(0)+\Delta t)^(2)`

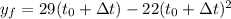
so we can rewrite our formula as:

`\overline{v}=(29(t_(0)+\Delta t)-22(t_(0)+\Delta t)^(2)-y_(0))/(\Delta t)`

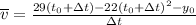
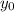`y_(0)` will always be the same, so we can start by calculating that, we take the provided function ans evaluate it for t=1s, so we get:

`y_(0)=29t-22t^(2)`

`y_(0)=29(1)-22(1)^(2)`

`y_(0)=7ft`

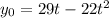
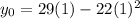
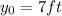
we can substitute it into our average velocity equation:

`\overline{v}=(29(t_(0)+\Delta t)-22(t_(0)+\Delta t)^(2)-7)/(\Delta t)`

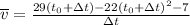
and we also know that the initil time will always be 1, so we can substitute it as well.

`\overline{v}=(29(1+\Delta t)-22(1+\Delta t)^(2)-7)/(\Delta t)`

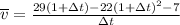
so we can now simplify our formula by expanding the numerator:

`\overline{v}=(29+29\Delta t-22(1+2\Delta t+\Delta t^(2))-7)/(\Delta t)`

`\overline{v}=(29+29\Delta t-22-44\Delta t-22\Delta t^(2)-7)/(\Delta t)`

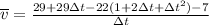
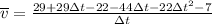
we can now simplify this to:

`\overline{v}=(-15\Delta t-22\Delta t^(2))/(\Delta t)`

Now we can factor Δt to get:

`\overline{v}=(\Delta t(-15-22\Delta t))/(\Delta t)`

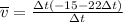
and simplify

`\overline{v}=-15-22\Delta t`

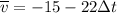
Which is the equation that will represent the average speed of the ball. So now we can substitute each period into our equation so we get:

`\overline{v}_(@\Delta t=0.01s)=-15-22(0.01)=-15.22ft/s`

`\overline{v}_(@\Delta t=0.005s)=-15-22(0.005)=-15.11ft/s`

`\overline{v}_(@\Delta t=0.002s)=-15-22(0.002)=-15.044ft/s`

`\overline{v}_(@\Delta t=0.001s)=-15-22(0.001)=-15.022ft/s`