The expected length of code for one encoded symbol is
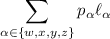
where
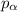 is the probability of picking the letter
is the probability of picking the letter
 , and
, and
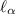 is the length of code needed to encode
is the length of code needed to encode
 .
.
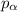 is given to us, and we have
is given to us, and we have
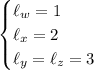
so that we expect a contribution of
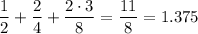
bits to the code per encoded letter. For a string of length
 , we would then expect
, we would then expect
![E[L]=1.375n](https://img.qammunity.org/2020/formulas/mathematics/college/hqm1c10fn6qzgumjabpe2bwoo2g7aqikcg.png) .
.
By definition of variance, we have
![\mathrm{Var}[L]=E\left[(L-E[L])^2\right]=E[L^2]-E[L]^2](https://img.qammunity.org/2020/formulas/mathematics/college/x1ainur8rb09lpvs0v7y9bzd0b7ueskpaj.png)
For a string consisting of one letter, we have
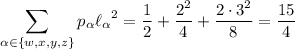
so that the variance for the length such a string is
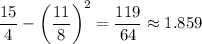
"squared" bits per encoded letter. For a string of length
 , we would get
, we would get
![\mathrm{Var}[L]=1.859n](https://img.qammunity.org/2020/formulas/mathematics/college/pwuiriygj71he1t3chjwx0it77om1l5zbf.png) .
.