Question

Scientists released 5 foxes into a new habitat in year 0. Each year, there were

four times as many foxes as the year before. How many foxes were there
after x years? Write a function to represent this scenario.

Answer 1

`f(x)= 5*4^x`

Explanation:

Since every year there are four times as many foxes as the year before, every year we need to multiply the previous population by 4. This leads to having to multiply by
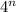`4^(n)`after n years have gone by. So we are in the presence of a population growth that goes as an exponential function of base "4".

A function f(x) that represents an exponential growth of such type can be written as:

`f(x)= N_0 * 4^x`

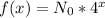
where x represents the variable time in years, 4 is the multiplicative base, and
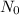`N_0` is what is defined as the "initial value" of the population (in our case 5 - for the 5 foxes initially released).

Notice also that when we start counting - time zero (x=0) the exponential form
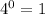`4^0 = 1` becomes a one (1) and the expression reduces to this initial value
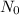`N_0` (5 in our case).

Therefore, the function representing this population growth is:
`f(x)= 5*4^x`