Question

An = An-1-3 when a1 = 5

Answer 1

Consider we need to find the first five terms of the given AP and the explicit formula.

Given:

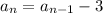`a_n=a_(n-1)-3` when
`a_1=5`

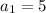
To find:

First five terms of the given AP and the explicit formula.

Solution:

We have,

`a_n=a_(n-1)-3` ...(i)

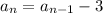`a_1=5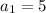`, it means first term is 5.

Putting n=2 in (i), we get

`a_2=a_(2-1)-3`

`a_2=a_(1)-3`

`a_2=5-3`

`a_2=2`

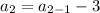
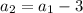
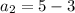
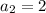
Second term is 2. So, common difference is

`d=a_2-a_1`

`d=2-5`

`d=-3`

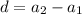
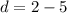
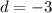
First terms is 5 and common difference is -3. So, the first five terms of the AP are 5, 2, -1, -4, -7.

The explicit formula of an AP is

`a_n=a_1+(n-1)d`

`a_n=5+(n-1)(-3)`

`a_n=5-3n+3`

`a_n=8-3n`

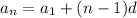
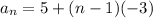
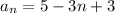
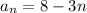
Therefore, the explicit formula of AP is
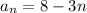`a_n=8-3n`.