Question

The probabilities of poor print quality given no printer problem, misaligned paper, high ink viscosity, or printer-head debris are 0, 0.3, 0.4, and 0.6, respectively. The probabilities of no printer problem, misaligned paper, high ink viscosity, or printer-head debris are 0.8, 0.02, 0.08, and 0.1, respectively.

a. Determine the probability of high ink viscosity given poor print quality.
b. Given poor print quality, what problem is most likely?

Answer 1

Answer of Part(a) is 16/49

and Answer of Part(b) is Printer-head debris

Explanation:

Answer is in the following attachment

Answer 2

Answer and explanation:

Given : The probabilities of poor print quality given no printer problem, misaligned paper, high ink viscosity, or printer-head debris are 0, 0.3, 0.4, and 0.6, respectively.

The probabilities of no printer problem, misaligned paper, high ink viscosity, or printer-head debris are 0.8, 0.02, 0.08, and 0.1, respectively.

Let the event E denote the poor print quality.

Let the event A be the no printer problem i.e. P(A)=0.8

Let the event B be the misaligned paper i.e. P(B)=0.02

Let the event C be the high ink viscosity i.e. P(C)=0.08

Let the event D be the printer-head debris i.e. P(D)=0.1

and the probabilities of poor print quality given printers are

`P(E|A)=0,\ P(E|B)=0.3,\ P(E|C)=0.4,\ P(E|D)=0.6`

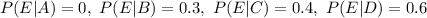
First we calculate the probability that print quality is poor,

`P(E)=P(A)P(E|A)+P(B)P(E|B)+P(C)P(E|C)+P(D)P(E|D)`

`P(E)=(0)(0.8)+(0.3)(0.02)+(0.4)(0.08)+(0.6)(0.1)`

`P(E)=0+0.006+0.032+0.06`

`P(E)=0.098`

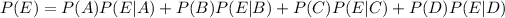
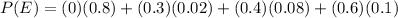
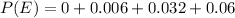
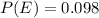
a. Determine the probability of high ink viscosity given poor print quality.

`P(C|E)=(P(E|C)P(C))/(P(E))`

`P(C|E)=(0.4* 0.08)/(0.098)`

`P(C|E)=(0.032)/(0.098)`

`P(C|E)=0.3265`

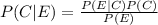
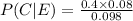
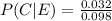
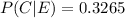
b. Given poor print quality, what problem is most likely?

Probability of no printer problem given poor quality is

`P(A|E)=(P(E|A)P(A))/(P(E))`

`P(A|E)=(0* 0.8)/(0.098)`

`P(A|E)=(0)/(0.098)`

`P(A|E)=0`

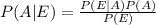
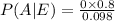
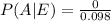
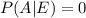
Probability of misaligned paper given poor quality is

`P(B|E)=(P(E|B)P(B))/(P(E))`

`P(B|E)=(0.3* 0.02)/(0.098)`

`P(B|E)=(0.006)/(0.098)`

`P(B|E)=0.0612`

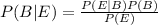
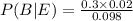
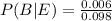
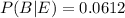
Probability of printer-head debris given poor quality is

`P(D|E)=(P(E|D)P(D))/(P(E))`

`P(D|E)=(0.6* 0.1)/(0.098)`

`P(D|E)=(0.06)/(0.098)`

`P(D|E)=0.6122`

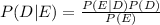
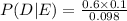
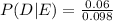
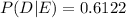
From the above conditional probabilities,

The printer-head debris problem is most likely given that print quality is poor.