The equation
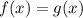 is
is

Some observations:
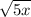 is defined only as long as
is defined only as long as
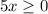 , or
, or
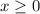
- wherever
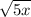 is defined, its value must be non-negative, so that
is defined, its value must be non-negative, so that
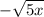 is never positive
is never positive - by the definition of absolute value, we have
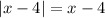 if
if
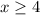 , and
, and
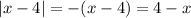 if
if
 . Then
. Then
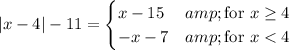
If
 , the equation becomes
, the equation becomes
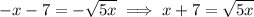
Taking the square of both sides gives
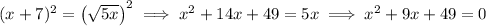
but since the discriminant is
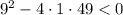 , there are no real solutions.
, there are no real solutions.
If
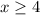 , then
, then
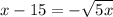
Taking squares gives
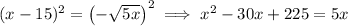
and solving by the quadratic formula gives two potential solutions,
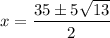
which have approximate values of 8.49 and 26.51.
We know for any value of
 that
that
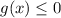 . We have
. We have
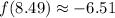 and
and
 , so only the first solution 8.49 is valid.
, so only the first solution 8.49 is valid.