Question

According to the universal law of gravitation, if you triple the distance between two objects, then the gravitational force between them __________. According to the universal law of gravitation, if you triple the distance between two objects, then the gravitational force between them __________.

decreases by a factor of 9
increases by a factor of 9
decreases by a factor of 3
increases by a factor of 3

Answer 1

According to the universal law of gravitation, if you triple the distance between two objects, then the gravitational force between them decreases by a factor of 9.

Step-by-step explanation:

The universal law of gravitation is defined as:

`F = G(m1m2)/(r^(2))`

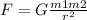
Where G is the gravitational constant, m1 and m2 are the masses of the two objects and r is the distance between them.

The gravitational force will decrease if the square of the distance between the two object increases, that means that the force (F) and the distance (r) are inversely proportional.

Putting the scenario at which it triples the distance between the two objects, the universal law of gravitation will be described as:

`F = G(m1m2)/((3r)^(2))`

`F = G(m1m2)/(9r^(2))`

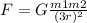
Since the force and the distance are inversely proportional, the gravitational force between the two objects decreases by a factor of 9.