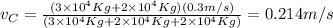Question

(a) A load of coal is dropped (straight down) from a bunker into a railroad hopper car of inertia 3.0 × 104 kg coasting at 0.50 m/s on a level track. The car’s speed is 0.30 m/s after the coal lands on it. Use this to determine the inertia of the load of coal. (b) If right after after this a second load of coal (of the same mass) is dropped into the same car, what will be the new final speed of the car?

Answer 1

a) m=20000Kg

b) v=0.214m/s

Step-by-step explanation:

We will separate the problem in 3 parts, part A when there were no coals on the car, part B when there is 1 coal on the car and part C when there are 2 coals on the car. Inertia is the mass in this case.

For each part, and since the coals are thrown vertically, the horizontal linear momentum p=mv must be conserved, that is,
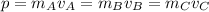`p=m_Av_A=m_Bv_B=m_Cv_C`, were each velocity refers to the one of the car (with the eventual coals on it) for each part, and each mass the mass of the car (with the eventual coals on it) also for each part. We will write the mass of the hopper car as
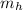`m_h`, and the mass of the first and second coals as
`m_1` and
`m_2` respectively

We start with the transition between parts A and B, so we have:

`m_Av_A=m_Bv_B`

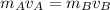
Which means

`m_hv_A=(m_h+m_1)v_B`

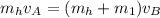
And since we want the mass of the first coal thrown (
`m_1`) we do:

`m_hv_A=m_hv_B+m_1v_B`

`m_hv_A-m_hv_B=m_1v_B`

`m_1=(m_hv_A-m_hv_B)/(v_B)=(m_h(v_A-v_B))/(v_B)`

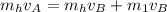
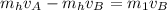
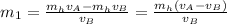
Substituting values we obtain

`m_1=((3*10^4Kg)(0.5m/s-0.3m/s))/(0.3m/s)=20000Kg=2*10^4Kg`

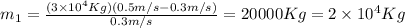
For the transition between parts B and C, we can write:

`m_Bv_B=m_Cv_C`

Which means

`(m_h+m_1)v_B=(m_h+m_1+m_2)v_C`

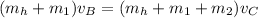
Since we want the new final speed of the car (
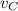`v_C`) we do:

`v_C=((m_h+m_1)v_B)/((m_h+m_1+m_2))`

Substituting values we obtain

`v_C=((3*10^4Kg+2*10^4Kg)(0.3m/s))/((3*10^4Kg+2*10^4Kg+2*10^4Kg))=0.214m/s`