Question

Water is poured into a conical paper cup at the rate of 3/2 in3/sec (similar to Example 4 in Section 3.7). If the cup is 6 inches tall and the top has a radius of 3 inches, how fast is the water level rising when the water is 4 inches deep?

Answer 1

The water level rising when the water is 4 inches deep is
`(3)/(8* \pi) inch/s`.

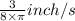Explanation:

Rate of water pouring out in the cone = R=
`(3)/(2) inch^3/s`

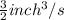
Height of the cup = h = 6 inches

Radius of the cup = r = 3 inches

`(r)/(h)=(3 inch)/(6 inch)=(1)/(2)`

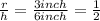
r = h/2

Volume of the cone =
`V=(1)/(3)\pi r^2h`

`V=(1)/(3)\pi r^2h`

`(dV)/(dt)=(d((1)/(3)\pi r^2h))/(dt)`

`(dV)/(dt)=(d((1)/(3)\pi ((h)/(2))^2h))/(dt)`

`(dV)/(dt)=(1)/(3* 4)\pi * (d(h^3))/(dt)`

`(dV)/(dt)=(1\pi )/(12)* 3h^2* (dh)/(dt)`

`(3)/(2) inch^3/s=(1\pi )/(12)* 3h^2* (dh)/(dt)`

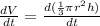
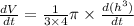
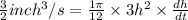
h = 4 inches

`(3)/(2) inch^3/s=(1\pi )/(12)* 3* (4inches )^2* (dh)/(dt)`

`(3)/(2) inch^3/s=\pi* 4* (dh)/(dt) inches^2`

`(dh)/(dt)=(3)/(8* \pi) inch/s`

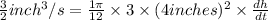
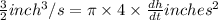
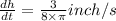
The water level rising when the water is 4 inches deep is
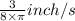`(3)/(8* \pi) inch/s`.