Question

In the 1991 World Track and Field Championships in Tokyo, Mike Powell jumped 8.95 m, breaking by a full 5 cm the 23-year long-jump record set by Bob Beamon . Assume that Powell's speed on takeoff was 9.5 m/s (about equal to that of a sprinter) and that g = 9.80 m/s2 in Tokyo. How much less was Powell's horizontal range than the maximum possible horizontal range for a particle launched at the same speed?

Answer 1

0.26 m

Step-by-step explanation:

θ = Angle at which the jumper launched

g = Acceleration due to gravity = 9.8 m/s²

R = Range = 8.95 m

v = Velocity of the jumper = 9.5 m/s

Range of projectile

`R=\frac {v^(2)\sin 2\theta}{g}`

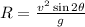
When, θ = 45° maximum range is obtained

sin(2×45) = sin90 = 1

Maximum range

`R_m=(v^2)/(g)\\\Rightarrow R_m=(9.5^2)/(9.8)\\\Rightarrow R_m=9.21\ m`

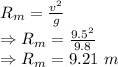
So, Mike Powell jumped 9.21-8.95 = 0.26 m less than the maximum range if launched at the same speed.