Question

A seashell has only 3.1% of its c-14 left. The half life of c-14 is 5740 years. How old is the seashell

Answer 1

The seashell is 28747.96 years old.

Why?

If we need to calculate how old is something, we can use the equation for radioactive decay rate. It's possible using the C-14 half-life (5740 years) as reference. Remember, C-14 is used because all the living things take up the element from the atmosphere, when an organism dies, the amount of carbon starts to decay (very slowly).

Decay rate half life:

`N_(t)=N_(o)*e^(-l*t)`

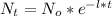
Where,

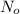`N_o}` is the initial number of atoms (undecayed)

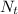`N_(t)` is the the number of atoms at time (undecayed)

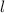`l` is the decay rate

Now, isolating the decay rate of the formula, we have:

{
`N_(t)=N_(o)*e^(-l*t)\\\\ln((N_(t))/(N_(o)))=-l*t\\`

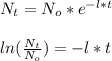
Also, we can get the value of the decay rate (half life), using the following formula:

`l=(0.693)/(5740)=1.207x10^(-4)`

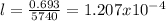
Then, using the given information, we have:

`ln((3.1)/(100))=-1.207x10^(-4)*t`

`-3.47=-1.207x10^(-4)*t`

`-3.47=-1.207x10^(-4)*t\\\\t=(-3.47)/(1.207x10^(-4))=28748.96years`

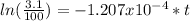
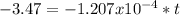
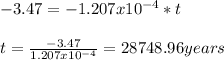
Hence, the seashell is 28748.96 years old.

Have a nice day!