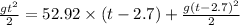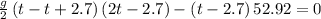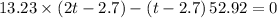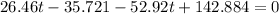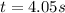Question

A stone falls from rest from the top of a cliff. A second stone is thrown downward from the same height 2.7 s later with an initial speed of 52.92 m/s. They hit the ground at the same time. How long does it take the first stone to hit the ground? The acceleration of gravity is 9.8 m/s 2 .

Answer 1

Answer:4.05 s

Step-by-step explanation:

Given

First stone is drop from cliff and second stone is thrown with a speed of 52.92 m/s after 2.7 s

Both hit the ground at the same time

Let h be the height of cliff and it reaches after time t

`h=(gt^2)/(2)`

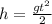
For second stone

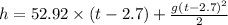`h=52.92* \left ( t-2.7\right )+(g\left ( t-2.7\right )^2)/(2)`---2

Equating 1 &2 we get

`(gt^2)/(2)=52.92* \left ( t-2.7\right )+(g\left ( t-2.7\right )^2)/(2)`

`(g)/(2)\left ( t-t+2.7\right )\left ( 2t-2.7\right )-\left ( t-2.7\right )52.92=0`

`13.23* \left ( 2t-2.7\right )-\left ( t-2.7\right )52.92=0`

`26.46t-35.721-52.92t+142.884=0`

`t=4.05 s`