Answer:
a. ≈ 1.22449s
b. ≈ 14.69387m
c. ≈ 0.532415s
Step-by-step explanation:
Because we are trying to find when it is at it's highest point we can safely say that it's velocity at that point is 0m/s,
therefore we can use the equation:
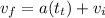
and do some algebra to get:
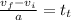
Now we plug in our values (note that this is assumed to be on Earth and that because it says that upwards is positive, we set g to be negative to say that it is pointing down):
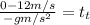
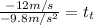
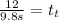
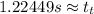
To find the final height we can use:
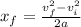
and plug in our values to get:
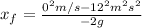
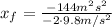
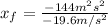
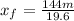
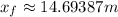
To find the time we can use the time dependent position equation:
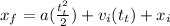
This here can be made into a quadratic equation like so (xi is set up to be 0m, so the equation wont have it):
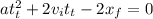
Here we can use the quadratic formula:
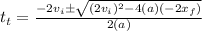
And now it would be best if we put in our values (xf = 5m because that is our question):
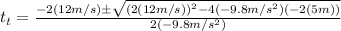
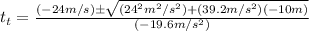
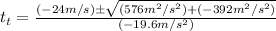
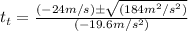
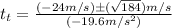
Finally we have simplified enough to be worth solving for:
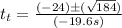
We get:
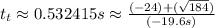
and
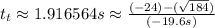
Because time is always positive we want to choose the plus answer.