Question

Suppose the time it takes for a purchasing agent to complete an online ordering process is normally distributed with a mean of 8 minutes and a standard deviation of 2 minutes. Suppose a random sample of 25 ordering processes is selected. What is the standard deviation of the sampling distribution of mean​ times? (Round to one decimal place.)

Answer 1

Answer: 0.4

Explanation:

We know that the standard deviation of the sampling distribution of mean​ is given by:-

`\sigma_x=(\sigma)/(√(n))`

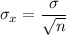
Given : Standard deviation :
`\sigma= 2\text{ minutes}`

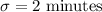
Sample size : n= 25

Then, the standard deviation of the sampling distribution of mean​ times will be :-

`\sigma_x=(2)/(√(25))\\\\\Rightarrow\ \sigma_x=(2)/(5)=0.4`

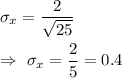
Hence, the standard deviation of the sampling distribution of mean​ times=0.4