Answer: 0.4
Explanation:
We know that the standard deviation of the sampling distribution of mean is given by:-

Given : Standard deviation :

Sample size : n= 25
Then, the standard deviation of the sampling distribution of mean times will be :-
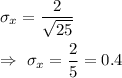
Hence, the standard deviation of the sampling distribution of mean times=0.4