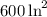ANSWER:
The area of the triangular road sign is
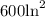
SOLUTION:
We need to find the area of the road sign, which is in triangular shape.
So, we need to calculate the area of a triangle.
Given, length of the base of the given triangle = 30 inches
Height of the given triangle = 40 inches
We know that,
area of the triangle
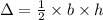
Where,
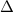 = area of a triangle
= area of a triangle
b = base length of the triangle
h = height of the given triangle
hence substituting the values we get
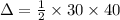
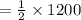
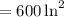
Hence, the area of the triangular road sign with base of 30 inches and a height of 40 inches is