Answer:
Radius = 9.0216 cm
Step-by-step explanation:
Given that:
The critical mass of neptunium-237 = 60 kg
Also, 1 kg = 1000 g
So mass = 60000 g
Density = 19.5 g/cm³
Volume = ?
So, volume:

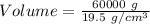
The volume of the material = 3076.92308 cm³
The expression for the volume of the sphere is:


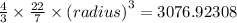
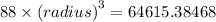
![{(radius)}=\sqrt[3]{(64615.38468)/(88)}](https://img.qammunity.org/2020/formulas/physics/high-school/248kwf67i2h2bxg4wpft464t3rmebsrs8i.png)
Radius = 9.0216 cm